A true intuition on looking at the sky: Brauner’s “Surrealist” and Georg Cantor
Posted: December 28, 2011 Filed under: People, Philosophy, Visual Arts | Tags: Andre Breton, Art, Bertrand Russell, Cardinal numbers, David Hilbert, Georg Cantor, Henri Poincare, Infinity, John Horton Conway, John Wallis, Jorge Luis Borges, Kurt Godel, Leopold Kronecker, Ludwig Wittgenstein, M.C. Escher, Mathematics, Max Bill, Mobius strip, Paradox, Paul J. Cohen, Philosophy, Salvador Dali, Surreal numbers, Surrealism, Theology, Victor Brauner, Visual Arts, Zeno 1 CommentVictor Brauner’s “Surrealist”
In a 1924 “surrealist manifesto”, André Breton (1896 – 1966) declared Surrealism to be the “dictation of thought in the absence of all control exercised by reason“. Salvador Dali (1904 – 1989), the emblematic figure of Surrealism, rephrased this by admitting that “the only difference between a madman and me is that I am not mad“. Indeed, like a conjurer or magician the surrealist has to perform the trick of expressing “the real functioning of thought” by crossing the line of reason while retaining all the while his own sanity. And this is exactly how the Romanian painter Victor Brauner (1903 – 1966) pictured his own “Surrealist” (1947), a conjurer ready to do his tricks within a mad and undecipherable world. The instruments of his craft appear scattered upon a strange, half – animate table, objects that one would normally expect to find either in a magician’s tool box or in a priest’s case. Across his oversized, eccentric hairdo the symbols of the Beginning and the End, an aleph and a lemniscate, appear as an attempt to convey some metaphysical, enigmatic message. Brauner’s painting, evidently inspired by the tarot card of the “magician”, bears the mark of the painter’s keen interest in the occult yet, by a quite remarkable concurrence, the association of the painting to a surrealist transforms the composition into a mathematical rebus.
The lemniscate and the aleph
In M.C. Escher’s engraving “Ants”, a procession of ants is presented performing a potentially perpetual march upon a Möbius – like strip, a one – sided surface produced by twisting and joining the ends of a strip or ribbon. In a number of other engravings, Escher toyed with infinity by employing several variations of the same idea, twisted ribbons implying an endless route. The German graphic artist Max Bill (1908 – 1994) was similarly inspired by this representation and in his aptly titled sculpture “Endless Ribbon” (1935) made an elegant comment on the twisted ribbon as a symbol of infinity.
The lemniscate (Greek “λημνίσκος” and Latin “lemniscus”, translated as “ribbon”), the symbol that after John Wallis’ “De Sectionibus Conicis” (On Conic Sections, 1655) came to denote infinity in Mathematics, may thus well be the most representational mathematical symbol. Indeed it may be thought of as a stylized version of a twisted ribbon forming an eight – shaped loop, aptly communicating the notion of endlessness, in a manner not very different than Escher’s “Ants” or Bill’s “Ribbon”. Brauner’s lemniscate appears under “aleph”, the first letter of the early Phoenician script in its Hebrew version, a symbol shared by many other scripts and that, after a succession of historical osmoses covering a time span of three millennia, was passed through to the Greek (alpha), Latin and Cyrillic alphabets. Aleph naturally became the symbol of the beginning and corresponded to number 1 in gematria, the occult belief that assigning numbers to letters may provide insight and reveal the words’ concealed meaning. Yet it was the German mathematician Georg Cantor (1845 – 1918) who raised aleph well beyond its linguistic, historical or even mystical sphere and connected it to infinity, crossing the line of conventional reasoning while struggling all the while to retain his own sanity.
Cantor’s paradise
David Hilbert’s emblematic words of a “paradise” created by Georg Cantor and from which “no one can expel” devoted mathematicians are indicative of both the deep impact and the acute conflict Cantor’s ideas about infinity stirred in the mathematical world. With Cantor, infinity was raised from a rather vague intuitive notion to a rule governed, structured hierarchy, itself potentially infinite. Results of Cantor’s reasoning often appear as defying common sense and have provided notorious examples of Mathematics being counterintuitive. In a crescendo of bitter attacks by some of Cantor’s most prominent fellow mathematicians, Cantor became a “scientific charlatan”, a “renegade”, a “corrupter of truth” (Leopold Kronecker). The great Henri Poincaré (1854 – 1912) viewed Cantor’s “absurdities” as a “grave disease”, an infliction upon Mathematics while even decades after Cantor’s death, the Austrian philosopher Ludwig Wittgenstein (1889 – 1951) commented upon Cantor’s work on infinities as “pernicious”, “nonsense”, “wrong” and even “laughable”. It was even viewed as hubris towards Christian theology, questioning the very notion of the uniqueness of an absolutely infinite God. For if infinities, according to Cantor, can be hierarchically organized in a potentially endless sequence, then what could God’s absolute infiniteness possibly mean?
A part equivalent to the whole
At the core of Cantor’s ideas is the notion of a one to one correspondence between sets, an obvious and intuitive way of finding which one of two sets possesses more members than the other without having to count. To understand how this can be done, suppose that a large container is full of red and green apples. To find which of the two kinds of apples is more numerous, one has only to start picking one red and one green apple at a time, forming thus pairs of apples and establishing a one to one correspondence between the two sets. The result is reached when only apples of the same color are left in the container: at this point the one to one correspondence cannot continue further and the set to which the remaining apples belong is inaugurated as more numerous than the other. This process can sometimes yield results, albeit unexpected, even when applied to infinite sets. In such cases, one could not possibly expect one of the two sets to run out of members at some specific point, yet it could indicate that the one to one correspondence could proceed indefinitely, without leaving any of the members of the two sets out of the process. It would then appear natural to inaugurate the two sets as infinite and equally numerous, a result that at first does not appear paradoxical. However, it turns out that applying this process to an infinite set and one of its infinite subsets may occasionally yield that the two sets are equally numerous though one is a part of the other. A simple example is provided by the so called “Galileo’s paradox”, where a one to one correspondence is established between the natural numbers (0, 1, 2, 3, 4, 5, …) and their squares (0, 1, 4, 9, 16, 25, …) indicating that the two sets are “equally” infinite, though the latter appears to possess considerably fewer members than the former. A geometric equivalent is the obvious one to one correspondence between the points of two concentric circles, indicating that their points are equally numerous. Another striking example is the somewhat more complicated one to one correspondence between any line segment, of arbitrary length, and a line: both possess infinite points and are equally numerous, though the former is of finite length and the latter is of infinite length.
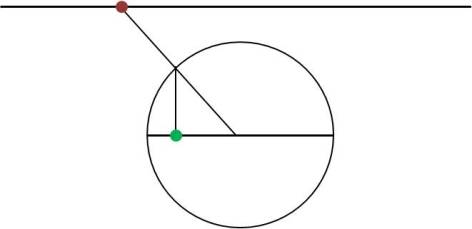
A one to one correspondence between the points of a line segment and the points of a straight line, leading to an apparent paradox: the two sets of points are infinite but “equally numerous”. Georg Cantor assigned to this type of infinity the cardinal number “aleph one”.
A procession of alephs
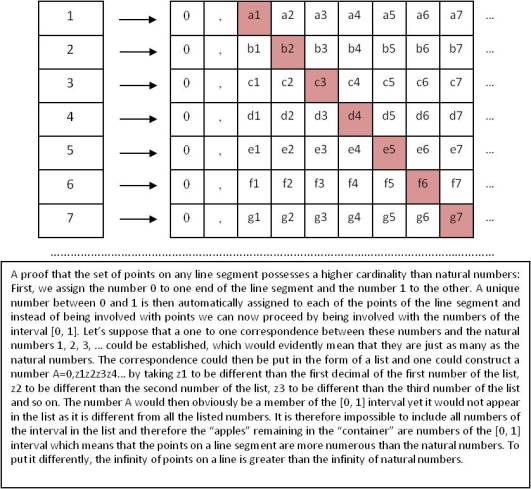
What appears more remarkable is the fact that, following the same procedure of establishing one to one correspondences between sets, one could arrive to the result that some infinite sets are more numerous than other infinite sets. An ingenious “diagonal” argument and Zeno’s “reductio ad absurdum” (proof by contradiction) may be employed to prove that the number of points on a line segment is more numerous than the natural numbers, though both are infinite. Cantor denoted the former “aleph naught” (or “aleph null”) and the latter “aleph one”, establishing the first two terms of a possible procession of alephs. It can be proved that the set of points on the whole plane correspond also to aleph one and thus, rather counter intuitively, the points on any line, the points on the plane, the numbers of any interval and the totality of the real numbers are all infinite yet equally numerous, placed one step up the “aleph naught” infinity of the natural numbers.
Georg Cantor, who referred to his alephs as “cardinal numbers”, struggled hard with the so called “continuum hypothesis”, the assertion that no other cardinal number exists between aleph naught and aleph one, without success. In 1938 Kurt Gödel (1906 – 1978) proved that the continuum hypothesis can be accepted without contradiction within the axiomatic system of set theory. Paul J. Cohen (1934 – 2007) took this a step further by proving in 1963 that one could also dismiss the continuum hypothesis without contradiction: another aleph could be assumed to exist between aleph naught and aleph one though no set corresponding to such a cardinal could be thought of. Cantor was able to prove that other sets, such as the set of all possible curves of the plane, have an even higher cardinal number than aleph one, which he called “aleph two”. In theory, one could proceed even further and discuss infinities with cardinal numbers “aleph three”, “aleph four” and so on ad infinitum, establishing an infinite procession of alephs. It is easy to confirm that the number of subsets of any set with n members is 2 raised to the power of n. Extending this result to infinite sets, one would expect that the number of subsets is 2 raised to the power of aleph naught. Using the diagonal argument, one may prove that this set of subsets is more numerous than the natural numbers and corresponds to a higher aleph, named aleph one. Proceeding on the same lines one may then discuss the set of subsets of an aleph one set to produce a set with cardinality aleph two and so on to produce sets with even higher cardinalities.
Surreal numbers
Brauner’s association of his mystical, lemniscate – crowned figure to a surrealist seems to take the allusion of the pictorial rebus a step further, towards the mind bending world of John Horton Conway’s (1937 -) “surreal” numbers. Conway’s system was first presented in Donald Knuth’s (1938 -) small novel aptly named “Surreal Numbers: How two ex – students turned on to pure Mathematics and found total happiness” (1974), a work of fiction unfold in the form of a dialogue. The core idea about constructing surreal numbers may at first appear simple enough, yet the immensity of Conway’s number continuum and the originality and eccentric nature of the numbers produced makes obvious why Knuth coined the term “surreal” to describe them (Conway himself actually named them, rather bluntly, simply “numbers”). The “surreal” universe is created in successive steps, or “days”, starting from scratch.
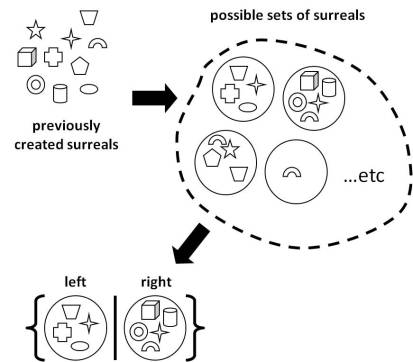
Every surreal number is thought of as the “gap” between two sets of numbers, each one consisting of surreal numbers created in previous steps. Thus, in each step of the process, previously defined surreals are used to form new sets which in turn are used to create new surreals ad infinitum. The scratch that initiates the process is simply the empty set, a set that contains nothing. The collection of surreal numbers thus produced, constitute an entity of immense “size”, called a “proper class”, and in which the real numbers are nothing more than a tiny molecule. Any surreal number x consists of two sets, one of which is called the left set (L) and the other is called the right set (R). To denote a surreal number produced by such two sets we use the symbol {L|R}. However in order to qualify as a surreal number, this entity must be such that no member of the right set is less than or equal to any member of the right set. Starting from the empty set ø, the only possible candidate is {ø|ø} or, in {|} in a more simple notation, which trivially qualifies as a surreal number and is named for convenience simply 0 i.e. 0={|}. This is the first surreal number and is created on day 0. Using this, one has now at hand ø and 0 as materials to construct the next generation of surreal numbers on day 1: these are {0|}, which is named 1, and {|0}, which is named -1 (notice that {0|0} does not qualify as a surreal). Numbers -2, -1/2, 1/2 and 2 are born on day 2, numbers -3, -1+1/2, -3/4, -1/4, 1/4, 3/4, 1+1/2, 3 are born on day 3 and so on, in an endless cosmogony that finally includes not only all ordinary, real numbers, rationals and irrationals, but also exotic entities involving Cantor’s alephs and mathematical operations.
A true intuition on looking at the sky
The harsh criticism aimed at the theory of cardinal numbers and the ad hominem attacks launched mainly by Kronecker, may have been the cause of the serious bout of depression Cantor suffered in 1884. As a result he had to interrupt his research and even consider been rather involved in pursuits irrelevant to Mathematics, deciding to address the Shakespearean authorship question. Though he returned to his research thereafter and even produced some of his most remarkable proofs, such as the diagonal argument, his condition remained shaken until the end of his life. During this period the stress kept increasing, as first his mother (October 1896), then his younger brother (January 1899) and finally his 13 year old son (December 1899) died. Until his retirement in 1913, Cantor struggled hard with mental illness and was hospitalized several times while at the same time he had to endure the malnourishment imposed by war condition in Germany. In 1917 he entered a sanatorium from where he regularly wrote to his wife, asking for a permission to go home, until he finally died in 1918. Though during his life he received only modest honors, his alephs and his ingenious proofs are now universally accepted and acknowledged as gems of almost artistic beauty. Victor Brauner most probably intended his “Surrealist” differently, obviously linking it to the tarot card of the “magician”, yet viewing it now it is hard not to think of Cantor, especially as the concurrence is so strongly underlined by the lemniscate and the aleph. The picture is after all about a conjurer, a “charlatan” in his “paradise”, to use Kronecker’s and Hilbert’s words, a “surrealist” who is struggling to retain his sanity. Even the tarot interpretation of the “magician” speaks of knowledge brought out of the darkness and the potential of an adventure to explore the world and eventually learn the fundamental elements of the Universe. And what is more fundamental in the Universe than infinity? “I suspect that the word infinite” said Jorge Luis Borges, “was at one time the insipid equivalent of unfinished; today it is one of God’s perfections in Theology, a cause of argument in Metaphysics, as well as a popular point of emphasis in Literature, a revived abstract concept in Mathematics – Russell explains the addition, multiplication and raising of cardinal numbers to infinite powers and the reason for their almost terrible dynasties – and a true intuition on looking at the sky”. And though Cantor is not mentioned by name in this elegant paragraph, one should easily recognize his legacy behind Borges’ unusual wording of some “almost terrible dynasties”, the structured, potentially infinite hierarchy of alephs.



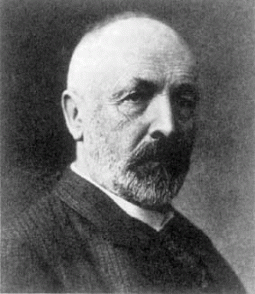
Reblogged this on Conceptual Art.