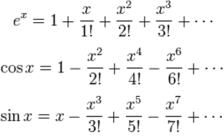The Mathematics of Max Ernst
Posted: December 27, 2010 Filed under: People, Visual Arts | Tags: Christian Zervos, Complex numbers, Dada, Decalcomania, Dupin cyclides, Euclid, Euler formula, Frottage, Geometry, Henri Poincare, Johannes Theodor Baargeld, Leonhard Euler, Loplop, Man Ray, Mathematics, Max Ernst, Pendulim, Rhodonea curves, Richard Feynman, Surrealism, Taylor expansion, Visual Arts 1 CommentArt that has nothing to do with Art
When the German artist Max Ernst (1891 – 1976) displayed some of his work at a Dusseldorf art exhibition, the daily press commented that “not even the best disposed of visitors knows what to make of these objects” and that Ernst had “regressed to a state of childhood to such an extent that he is now, in all seriousness, sticking old reels, cotton wool remains and wire together into ‘knotted sculptures’ along with dolls’ arms and legs, cogs and wheels from watches and whatever else is to be found in the junk – room”. In another occasion Ernst was even summoned at the headquarters of Cologne police where, together with the artist and poet Johannes Theodor Baargeld (1892 – 1927), he was accused as a fraud and scoundrel for “having demanded admission for something that was announced to the public as being an art exhibition, but which in reality has nothing to do with art”. Later, during the Nazi regime, works by Max Ernst were included in the 1937 “Entartete Kunst” (Degenerate Art) mockery exhibition, as examples of degradation in art.
In fact it was Ernst’s own decision and intention to move along the margin of conventional art: as a co-founder of the Cologne Dada group, together with Baargeld and Jean (Hans) Arp (1886 – 1966), he found himself for several years on the avant-garde of an anti-art movement that even flirted with nihilism. Though often hard to penetrate and certainly susceptible to many interpretations, Max Ernst’s work was both unconventional and ingenious. Much of it cannot even be described as painting or sculpture by a strict sense. He experimented with assemblages of unrelated objects and with collages comprised by printed material taken from book illustrations, advertisements and even various kinds of scientific textbooks. Ernst developed and extensively applied techniques of creating spontaneous images, compatible to surrealism, such as “frottage” (the creation of an image by rubbing a pencil on a paper stretched over a variety of materials). With “decalcomania” he applied color on the canvas using flat surfaces, such as glass, instead of brushes, achieving an unusual appearance of the finished surface, often disturbing, incompatible to the generally accepted notion of beauty, and sometimes likened to fractal structures. Against any conventional conception of art and against what is taught in art schools, Ernst often made use of a ruler and dividers to construct lines and forms in a geometrical – like manner.
The mathematical inspiration
Max Ernst displayed interest in Science and Mathematics that is certainly traceable in his artistic yield, both on the level of technique and on that of content. It is reported that, after a visit at the Henri Poincare Institute in Paris, he pointed out to Christian Zervos (1889 – 1970) , a Greek art critic and publisher of the Parisian “Cahiers d’ Art” magazine, a series of models on display, representing mathematical surfaces, that struck his imagination. This encounter brought these surfaces into the artistic surrealist foreground of the time and the American artist Man Ray (1890 – 1976), after a suggestion of Zervos, produced a series of photographs of these exhibits, under the title “Mathematical Objects”. Man Ray later described these surfaces as “so unusual, as revolutionary as anything that is being done today in painting or in sculpture”, though he admitted that he understood nothing of their mathematical nature. As curious objects, reminiscent of algebraic surfaces, appear in several of Ernst’s paintings, it is quite possible that he himself made attempts to incorporate them in his works. In “Design in Nature” (1947), a painting heavily influenced by Geometry and carried out using geometric technique, Ernst provides an allusion on the mathematical nature of the world’s design. In the background, a variety of shapes and curves give birth to living forms among alternating areas of light and dark. A mathematical solid, drenched in light, dominates the foreground topped by two horn – like structures, bringing to mind the “horn” or Dupin cyclides, two types of mathematical surfaces , forming thus an abstract ibex head. In the colorful “Feast of the Gods” (1948), a collection of surfaces and solids emerge amongst intense color rays of light, supposedly forming the monumental figures of the gods. Objects that could be thought of as their heads are again surfaces reminiscent of mathematical surfaces in Siamese – like complexes.
Pendulum instead of a brush
In several other works of Max Ernst, other mathematical curves appear that could be connected, rather unexpectedly, to the motion of a pendulum. The artist himself described his idea as follows:
“Tie an empty can to a piece of string one or two yards long and drill a small hole in its bottom. Now fill the can with paint and allow it to swing backwards and forwards over a flat canvas. Guide the can by movements of the hands, the arms, the shoulders and the whole body. In this way, amazing lines will trickle onto the canvas”.
Such lines are not very different than the rhodonea curves traced on the ground by a Foucault pendulum bob as seen directly from above. These curves are expressed in polar form by the equation r=coskθ, where the integer parameter k fixes the number of petals of the rhodonea and θ is a variable ranging from 0 to 2π.
In “Surrealism and Painting” (1942), the bird – like creature Loplop, Max Ernst’s alter ego that appears in several of his paintings, stretches an arm to the far right in order to draw lines bearing obvious resemblance to parts of a rhodonea curve. In “Euclid” (1945) a surrealist portrait of the ancient Geometer is presented in abstract form, the figure’s head rendered as a geometric solid, resembling a pyramid. The wise man is clad in noble, velvet clothes, rendered using the decalcomania technique, and adorned with two white roses. He is surrounded by a geometric background of overlapping planes, intersecting straight lines and rhodonea – like curves, some of which extend over its face, contributing to the formation of its features. His owl – like eyes, formed on an inverted antefix with the design of the ancient Greek anthemion ornament, glow bright yellow betraying intense intellectual activity. And then, in the obviously mathematical – inspired “Young Man Intrigued by the Flight of a Non – Euclidean Fly” (a picture executed in 1942 and colored in 1947), Max Ernst combined his Dupin cyclide surfaces and his exquisite, elegant pendulum curves to create a puzzling image of a creature resembling a bird (Loplop?) surrounded by the rhodonean trajectories of the “non – Euclidean” fly.

“Young Man Intrigued by the Flight of a Non – Euclidean Fly” (1942 – 1947). Above right: the horn, a parametric surface. Lower right: the rhodonea r=cos3θ
The imaginary unit of a revolutionary Art
In all the above instances Ernst alludes to Mathematics either by his experimental “dripping paint” technique or by the artistically unusual and revolutionary algebraic surfaces. Yet in the large painting “The Phases of the Night” (1946), a rare instance of explicit presence of mathematical symbols in a work of art is encountered. Over a night landscape of decalcomania, a bright moon appears in a form suggesting the phases of the moon from different points of view: an unusually oriented crescent supports what could be interpreted as a schematic representation of the lunar motion around the earth. A strange shape, formed by sinusoidal curves, casts its shadow over the moon. And similar sinusoidal curves, intimately related to circular and elliptic motion (and therefore inevitably connected to the motion of the moon), appear in various parts of the picture. The mountain range in the horizon and the strange dotted line unwinding from a circle in the foreground both display the same trigonometric function pattern. The most surprising feature of the painting is however the emergence of explicit mathematical symbols next to an owl – resembling creature with a glowing pair of eyes strongly reminiscent of the anthemion eyes of “Euclid”. A symbolic equation appears, involving a childishly painted heart and the imaginary unit i, or square root of -1, a peculiar number that came to Mathematics as a necessity during the 16th century, following the attempts to express the solutions of cubic and quartic polynomials in closed formulae. A deep and unexpected connection of the numbers containing this i, called complex numbers, to the exponential and trigonometric functions was first established by the great Leonhard Euler (1707 – 1783). This connection inevitably leads to what may be considered as the most remarkable equation of Mathematics and which appears in “The Phases of the Night” as the power i^i of complex analysis.
An allusion to Euler’s identity
Taylor series are representations of functions as infinite sums involving their derivatives calculated at a specific point and they are quite useful for approximating the values of a specific function by calculating the sum of a few initial terms. It is not difficult to construct such Taylor series for elementary functions such as the sine, the cosine and the exponential function.
In complex analysis these series may be extended to include imaginary powers, involving the imaginary unit i mentioned above. Using the imaginary power ix in the series of the exponential function, and the easily calculated powers of the imaginary unit, (i^0=1, i^1=i, i^2=-1, i^3=-i and so forth) the corresponding Taylor series is broken up in two parts, one formed by the terms of the sine series and one formed by the terms of the cosine series. This observation yields quite surprisingly, a relation between the exponential function and the trigonometric functions of sine and cosine, the notorious Euler formula e^(ix)=cosx+isinx.
A special case of this formula is derived for x=π producing thus an amazing result, the so called Euler’s identity: e^(iπ)+1=0. This relation connects some of the most fundamental mathematical constants (1, e, π and i) and has by many been described as a convincing yet unfathomable to its full meaning result. Richard Feynman described Euler’s identity as “a jewel” and “one of the most remarkable, almost astounding, formulas in all of Mathematics”.It is not hard to identify the relation between Max Ernst’s power i^i in the “Phases of the Night” and the Euler’s identity. As a matter of fact, it is a standard exercise in complex analysis and it takes only a little manipulation to see that for x=-π/2 Euler’s formula yields e^(iπ/2)=i. By raising both sides to the power i we arrive at the quite remarkable result i^i=e^(-π/2)=0,20788.
Though it is hard to see “what to make of this (mathematical) object” in “The Phases of the Night”, it is equally hard not to notice the repeated sinusoidal curves appearing in the painting and their connection to the Euler’s identity – and inevitably their connection to the i^i complex power. Moreover, the very title chosen by the artist, whose ordinary practice was to use the titles of his works as hints to the interpretation of his works, suggests a periodic alternation of cosmic proportions, governed by mathematical laws. It may not be coincidental that the specimens of mathematical jargon appear next to the aptly chosen, nocturnal owl, an ancient Greek symbol of wisdom. Its glowing eyes bring to mind the explicitly Mathematics – related painting of the Greek Geometer “Euclid”, painted only a year before. The mathematical nature of “The Phases of the Night” is further underlined by the dashed curve in the foreground, bringing to mind mathematical textbooks, by the square root symbol within the unwinding circular disk on the far left of the picture and by the vinculum inside the blue block on the far right.
It is quite uncertain whether Ernst was aware of the mathematical details accompanying his fragments of mathematical jargon in “The Phases of the Night”. It may be that he merely used mathematical cipher simply on a symbolic level in order to create an impression of mystery – and few accessible mathematical symbols could be considered as mysterious as the square root of -1. However, Mathematics is not simply a circumstantial occurrence in a few of his paintings but rather a lifelong influence and a structural element permeating his work as a whole. And having included mathematical symbols in a nocturnal, almost mystical landscape that, as explicitly confessed by its title, it is supposed to convey the idea of the cosmic design, is by itself an act of recognition of the admirable, metaphysical nature of the laws of the world’s design, reflected upon Mathematics.