Albrecht Dürer’s egg line

Artist and Geometer

In his treatise “Underweysung der Messung” (A Manual of Measurement) the German Rennaissance artist Albrecht Dürer begins with a homage to the ancient Greek geometer Euclid:

“The most sagacious of men, Euclid, has assembled the foundation of Geometry. Those who understand him well can dispense with what follows here…”

Thus Dürer, from the very first words of his Manual, makes clear that solid geometrical knowledge is indispensable in order to proceed to the study of the arts, and suggests to his readers to study Euclid first. In Dürer’s time painting was indeed starting to become geometric and analytical as much as artistic. Exact analytical methods had started to develop and the principles of linear perspective were being formulated and applied. Painting was becoming as much a freehand activity as a geometric, precise activity and, apart from brushes and paints, artists were starting to use rulers and dividers methodically. Dürer himself had even experimented with perspective devices allowing depiction of the subject from a specific point of view. An artist was therefore partly a geometer, using geometric instruments and applying geometric methods. Geometric knowledge became an essential element of artistic mastery.

Due to his affiliation to various mathematicians, Dürer had access to several mathematical texts and during his lifetime studied extensively Euclid’s “Elements”, including the very first printed edition and the first Latin translation from Greek (both published in Venice, 1482 and 1505 respectively). In “UdM” he makes an effort to present Geometric methods in a manner readily applicable to artists and craftsmen. No interest whatsoever is displayed on proof and pure geometric theory. Linear perspective, regular polygons, polyhedra and platonic solids are examined exclusively from a practical point of view and applications to typography, engineering and architecture are discussed.

Dürer’s construction of the ellipse

Page 30 of Albrecht Durer’s “Underweyssung der Messung”

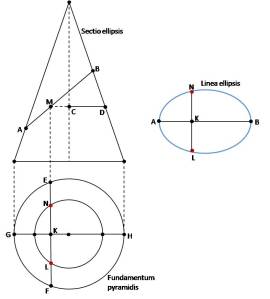
In page 30 of “UdM” Dürer presents a particularly interesting and rather complex method of constructing an ellipse. Elliptic shapes are indeed very important in painting and the visual arts, since every circle appears as an ellipse when viewed obliquely from a distance. For example, a circular plate on a table appears elliptic when viewed from anywhere in the room and appears circular only when viewed directly from above. Any ellipse possesses two symmetry axes, i.e. there are two ways for the ellipse to be folded in two identical halves. Nowadays, even amateur artists very early in their studies get accustommed to drawing elliptic shapes convincingly by freehand. However, an ellipse is a very specific set of points on a plane (a locus), possessing a certain mathematical property. Each point M of the ellipse is such that the sum of its distances from two fixed points remains constant. This definition of the ellipse provides also a very simple construction method, requiring only a pencil, two pins fixed on a board and a loop of string attached on them. For each positioning of the pins and each different string length, a different ellipse is generated. An exact elliptic shape can also be produced by applying an oblique cut to a right cone (i.e. a conic section). For example, the light cone of a tilted lampshade produces an elliptic shape on the ceiling. Dürer’s empirical construction of the ellipse makes use of exactly this property. The details of his method require a plan (i.e. a view from above) and an elevation (i.e. a side view) of a cone. Obviously, the elevation is an isosceles triangle and the plan is a circle with diameter equal to the base of the triangle. Dürer puts the circular plan right below the elevation, in absolute alignment, and labels them “fundamentum pyramidis” and “sectio ellipsis” respectively. The method proceeds as follows:

1. On the elevation, an oblique section is applied by drawing a line segment AB. Let M be any point of AB and CD be the corresponding radius of the cone.
2. A diameter GH of the circular plan is drawn, parallel to the base of the triangle. Let K be the projection of M on GH.
3. A vertical line EKF is drawn on the plan, where E, F are points of the circle. Then a concentric circle with radius CD is drawn and the intersection points N, L with line EKF are marked.
4. A third diagram (labeled “linea ellipsis”) is constructed, copying with dividers the oblique cut AB and the point M and adjusting a perpendicular line segment NML, equal to NKL. Points N, L are then two points of the ellipse.
5. The procedure is repeated for various points M on the oblique cut and thus various points of the ellipse are obtained.

Albrecht Duerer’s construction of eyer lini

Dürer’s construction produces only a discrete number of points of the ellipse: the gaps between them have to be filled in by freehand. In theory, the method is geometrically accurate. However, if it is supposed to serve for practical or artistic purposes it is certainly tedious, requiring a great amount of work and a great degree of accuracy in using the ruler and the dividers, only to produce a single ellipse.

The “eyer lini”

Remarkably, in Dürer’s own diagrams in “UdM”, it is more than obvious that his “linea ellipsis” is rather oval than elliptic, narrower in one side than the other and therefore possesses only one symmetry axis, resembling the shape of an egg. Dürer himself called the ellipse “the egg line” (eyer lini). Apparently, contrary to all evidence, and contrary to his own construction method, Dürer was convinced that the oblique section of a cone produces an egg shape. It can be safely presumed that, had Dürer fully realized the geometric properties of the ellipse, he would have taken specific care to make clear in his “Manual” the existence of a second symmetry axis.

By examining Dürer’s masterpieces, it can be seen that elliptic shapes sometimes stand out awkwardly. One of these instances can be observed in the central panel of the Dresden altarpiece (about 1498).

The central panel of the Dresden altarpiece

Despite the careful perspective and the geometric construction of the pavimento, it seems that the shape of the crown held obliquely by putti over Virgin’s head, which ought to be elliptic, is rather an arbitrary, elongated closed curve. A striking example that matches well the shape produced by Dürer in Udm is found in his notorious work “Melencolia I” (1514).  The bell hanging over the magic square displays exactly the same lack of the second symmetry axis and the characteristic oval shape of Dürer’s eyer lini.

A detail of “Melencolia I”

---